学习理论之感知器与最大间隔分类器
2014-10-16 13:14:00行业动态
到目前为止,我们使用的学习方法都是批量学习(batch learning)方式,即首先给定训练集学习出拟合假设函数中的参数,然后评价的效果的时候使用独立的测试集。本篇博文将会介绍一
到目前为止,我们使用的学习方法都是批量学习(batch learning)方式,即首先给定训练集学习出拟合假设函数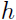 中的参数,然后评价
中的参数,然后评价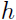 的效果的时候使用独立的测试集。本篇博文将会介绍一种在线学习(online learning)方式,即算法必须在学习的过程中不断地作出预测,而不是批量学习方式一样,学习过程结束后才作出预测。在线学习方式下,学习算法按顺序学习一个样本序列:
的效果的时候使用独立的测试集。本篇博文将会介绍一种在线学习(online learning)方式,即算法必须在学习的过程中不断地作出预测,而不是批量学习方式一样,学习过程结束后才作出预测。在线学习方式下,学习算法按顺序学习一个样本序列: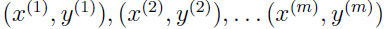 . 具体来讲就是,算法先根据
. 具体来讲就是,算法先根据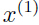 ,利用假设函数
,利用假设函数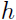 (参数首先初始化为某些较合适的值),给出
(参数首先初始化为某些较合适的值),给出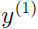 的预测值,预测完了之后,利用
的预测值,预测完了之后,利用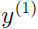 的实际值和预测值信息对参数进行更新;然后,在这个更新之后的参数的基础上,根据
的实际值和预测值信息对参数进行更新;然后,在这个更新之后的参数的基础上,根据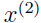 ,计算出
,计算出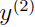 的预测值,再利用
的预测值,再利用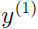 的实际值和预测值信息更新参数;如此重复下去直到最后一个样本。可以看出,在线学习只关注当前需要学习的样本所带来的误差,所以,在模型的应用过程就是学习参数过程中就需要不断预测,然后根据当前预测值与实际值的信息不断对参数做出调整。我们给出感知器算法的在线学习残差的一个边界。标签集采用
的实际值和预测值信息更新参数;如此重复下去直到最后一个样本。可以看出,在线学习只关注当前需要学习的样本所带来的误差,所以,在模型的应用过程就是学习参数过程中就需要不断预测,然后根据当前预测值与实际值的信息不断对参数做出调整。我们给出感知器算法的在线学习残差的一个边界。标签集采用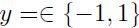 . 感知器的参数
. 感知器的参数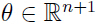 ,其中 n 是 x 的维度,参数之所以维度多了1,是因为,其中一个参数表示的是假设函数中的常数项,因此这个参数是没有 x 中某元素与之对应. 根据下面假设函数作出预测:
,其中 n 是 x 的维度,参数之所以维度多了1,是因为,其中一个参数表示的是假设函数中的常数项,因此这个参数是没有 x 中某元素与之对应. 根据下面假设函数作出预测: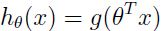 其中
其中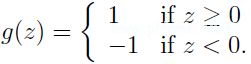 给出一个训练样本
给出一个训练样本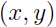 ,感知器学习规则就是,如果
,感知器学习规则就是,如果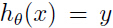 (即预测值和真实值相等),参数不作任何变化,如果不相等,用下面方式更新参数:
(即预测值和真实值相等),参数不作任何变化,如果不相等,用下面方式更新参数: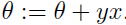
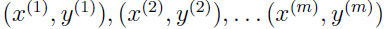 ,假设对于所有样本有
,假设对于所有样本有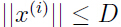
,进一步假设存在一个单位向量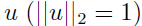 使得对于所有样本
使得对于所有样本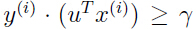 (即,当
(即,当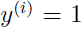 时,
时,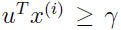 ,当
,当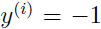 时,
时,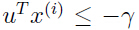 ,所以
,所以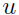 以最小间隔至少为
以最小间隔至少为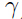 将数据分类),那么可以得出感知器算法在这个样本序列上的错误预测次数不超过
将数据分类),那么可以得出感知器算法在这个样本序列上的错误预测次数不超过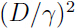 . 证明:由上面讨论可知,算法只在假设函数做出了错误的预测时才会更新参数. 用
. 证明:由上面讨论可知,算法只在假设函数做出了错误的预测时才会更新参数. 用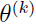 表第 k 次错误的权重,所以
表第 k 次错误的权重,所以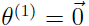 ,因为权重被初始化为0, 如果对于样本
,因为权重被初始化为0, 如果对于样本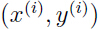 预测错误为第 k 个错误,那么
预测错误为第 k 个错误,那么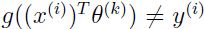 ,意味着:
,意味着: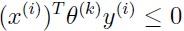 根据感知器学习规则,
根据感知器学习规则,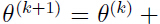
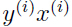 ,那么:
,那么: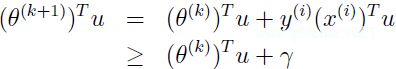
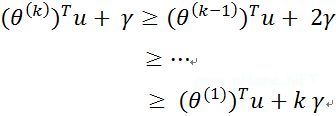
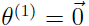 ,于是有:
,于是有: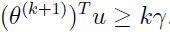 同样推理:
同样推理: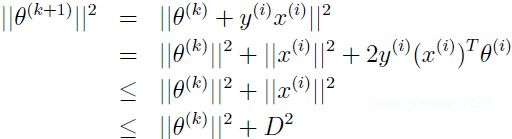
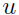 是单位向量(并且
是单位向量(并且 ,
, 是 z 和
是 z 和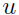 的夹角).上面推导出的结果表明
的夹角).上面推导出的结果表明 .
.
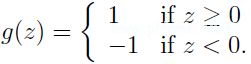 给出一个训练样本
给出一个训练样本下面的理论会给出感知器算法的在线学习错误预测次数的边界,以为每一次在线学习都会产生一个样本误差. 注意在线学习错误预测次数与样本数量和输入的维度之间没有依赖关系。
定理 (Block, 1962, and Noviko , 1962)给定样本序列,进一步假设存在一个单位向量
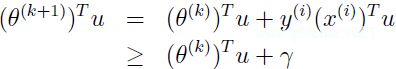
逐步递推有:
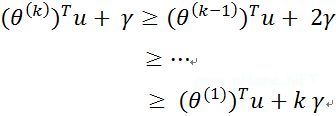
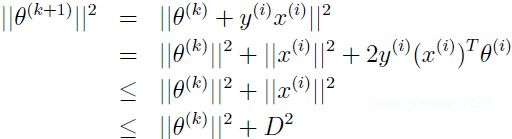
和上面一样的方法逐步递推可得到:![]() 由
由![]() 和
和![]()
一起可得到: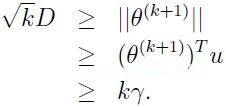
很赞哦! ()




 微信收款码
微信收款码 支付宝收款码
支付宝收款码